“Even though the primitives were no longer such, they remained a compositional criterion. For instance, given in first position the letter a, which refers to grammar, the depending letters have a mere distinctive value and refer back to grammatical sub-categories.
A third and final letter specifies a morphological termination or other derivation. Thus a list of terms is derived: ava (grammar), ave (letter), alve (vowel), adve (consonant) and so on. The expressions function like a chemical formula, which synthetically reveals the internal composition of its content, and like a mathematical expression in that the system attributes to each letter a value determined by its position.
Nevertheless, this theoretical perspicuity is bought at a dear price because, in practice, the lexicon becomes obsessively monotonous.
Equally, the Pasigraphie of De Maimieux institutes a graphic code of twelve characters that can be combined according to fixed rules. Each combination expresses a definite thought (the model is the Chinese character).
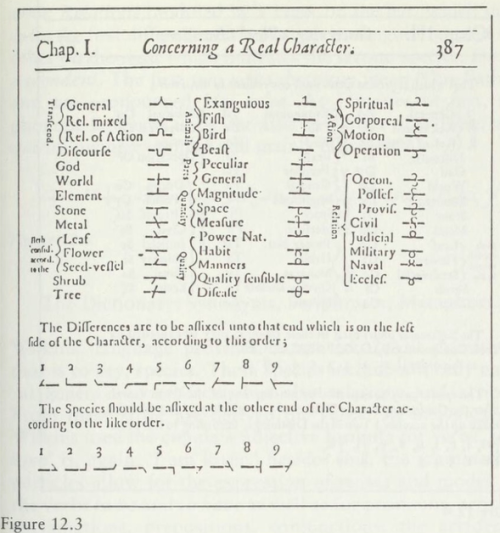
Other characters are placed on the outside of the “body” of the word to modify the central idea. The body of the word can contain three, four or five characters. Words of only three characters signify either “pathetic” terms or connectives linking parts of discourse, and are classified in an indicule.
Words of four characters stand for ideas in practical life (like friendship, kinship, business), and are classified in petit nomenclateur. Five character words concern categories such as art, religion, morality, science and politics, and are classified in a grand nomenclateur.
None of these categories is primitive; they have rather been isolated in terms of common sense as the most manageable way of subdividing contemporary knowledge. De Maimieux went so far as to admit that he had not sought for an absolute ordering but rather any ordering whatsoever, fût-il mauvais (p. 21).
The system, unfortunately, provides no way of eliminating synonyms; they are constitutional, and De Maimieux only says how to identify them. In fact, every expression in the pasigraphy can be connected not to a single meaning but to three or four different contents.
These different meanings can be distinguished according to the position of the characters on a sort of pentagram. This method imposes no small amount of tedium on the reader, who, as the characters display no iconic similarity with their content, is continually forced to consult the indicule, the petit nomenclateur or the grand nomenclateur, depending on the length of the expression.
Thus, to give an example, if we run across a five letter syntagm, we must seek first in the grand nomenclateur
“the class that begins with the first character of the term. Inside this class, we seek for the framework listing the second character of the term. Inside this framework, we seek for the column containing the third character of the term. Finding the right column, we seek the section (tranche) with the fourth character of the term.
Finally, within this section we seek the line containing the fifth character. At this point we will discover that, as the meaning, we have found a line listing four verbal words; it will then be necessary to observe which of the characters in the pasigraphic term is graphically tallest in order to determine which of the four possible words is the one corresponding to the term.” (Pellerey 1992a: 104).
A real piece of drudgery, though not enough to dampen the ardor of the project’s enthusiasts, who, starting with the abbé Sicard and finishing with various contemporary reviewers wishing to favor the diffusion of the system, entered into pasigraphic correspondence with each other and with De Maimieux, who even composed pasigraphic poetry.
De Maimieux spoke of his pasigraphy as an instrument for checking the accuracy of translations. Many theories of translation, in fact, presuppose the existence of a “parameter language” with which one can control the correct correspondence between the original text and the translated one.
De Maimieux aimed at proposing a supposedly neutral metalanguage which could track the correspondence between expressions in System A and those in system B. What was never placed in discussion was the fact that the content of this metalanguage was structured along the lines of Indo-European languages, and of French in particular.
As a consequence we have “the immense drama of ideography: it can identify and describe its contents, which are supposedly ideas or notions in themselves, only by naming them with words from a natural language–a supreme contradiction for a project created expressly to eliminate verbal languages.” (Pellerey 1992a: 114).
As can be seen, neither in technique nor in underlying ideology have we advanced very far from the time of Wilkins.
This disingenuousness is carried to paroxysms in the Palais de soixante-quatre fenêtres [ . . . ] ou l’art d’écrire toutes les langues du monde comme on les parle (1787, by the Swiss writer J.P. De Ria.
(Editorial note: Eco writes “De Ria,” yet Google returns “Jean-Pierre Deriaz” as the author of the work, and beautifully offers the 1787 document as a free eBook. Thank you, Google. Yet, history must agree with Eco, as the title page depicts the author as “J.P. De Ria,” as Eco attests.).
Despite its pretentious title, the book is nothing but a manual of phonetics or, perhaps, a proposal for the orthographic reform of French, written in a febrile, quasi-mystic style.
It is not in the least clear how the reform could be applied to all the languages of the world (it would, for example, be particularly inapplicable to English phonetics); but this is an unimaginable question for the author.
Returning to De Maimieux, the flexibility displayed in his choice of the pseudo-primitives seems to associate his project with the empiricist tendencies of the Encyclopédie; yet, once they were chose, his belief in them, and the self-confidence with which he sought to impose them on everyone else, still reflected the rationalist temperament.
In this respect, it is interesting to note that De Maimieux sought to provide for the rhetorical use of his language and the possibility of oratory: we are, of course, in a time of eloquence where the life or death of a revolutionary faction might depend on its ability to sway its audience by the force of its words.
Where the a priori linguists of the eighteenth-century were most critical of their predecessors, however, was in the matter of grammar. All were inspired by the “laconic” ideal proposed in the Encyclopédie.
In the grammar of De Maimieux, the number of grammatical categories originally projected by Faiguet is somewhat amplified; in the case of Delormel, however, the grammar is so laconic that Couturat and Leau (1903: 312), who spend long chapters describing other systems, liquidate his in a page and a half (Pellerey’s treatment is more accurate and generous; 1992a: 125).
Hourwitz, whose project remains akin to the seventeenth century polygraphies, produced a grammar that was, perhaps, the most laconic of all: one declension, one conjugation for verbs; the verbs were to be expressed in the infinitive with a few additional signs that specify tense and mood.
The tenses themselves were reduced to a system of three steps from the present, either backwards or forwards in time: thus A 1200 means “I dance;” A/1200 means “I have danced;” A 1200/ means “I will dance.”
If the grammar was made laconic, it followed that the syntax needed to be drastically simplified as well; Hourwitz proposed retaining the direct word order of French. In this respect, the relevance of Count Antoine de Rivarol’s pamphlet, De l’universalité de la langue française (1784), becomes apparent.
What was the need for a universal language, asked the count, when a perfect language existed already? The language was, of course, French. Apart from its intrinsic perfection, French was already an international language; it was the language most diffused in the world, so much that it was possible to speak of the “French world” just as, in antiquity, one could speak of the “Roman world.” (p. 1).
According to de Rivarol, French possessed a phonetic system that guaranteed sweetness and harmony, as well as a literature incomparable in its richness and grandeur; it was spoken in that capital city which had become the “foyer des étincelles répandues chez tous les peuples” (p. 21).
In comparison with French all other languages paled: German was too guttural, Italian too soft, Spanish too redundant, English too obscure. Rivarol attributed the superiority of French to its word order: first subject, then verb, and last object. This word order mirrored a natural logic which was in accordance with the requirements of common sense.
This common sense is, however, linked to the higher activity of our minds: for if we were to base our syntactical order on the order of our perceptions, it is plain that we would start with the object, which first strikes our senses.
The polemical reference to the sensationalism of Condillac is evident when de Rivarol asserts that, if other people, speaking in other tongues, had abandoned the natural, direct word order, it was because they had let their passions prevail over their intellect (p. 25-6).
This retreat from natural reason, moreover, was responsible for the syntactic inversion that had provoked the confusions and ambiguities prevalent in natural languages other than French. Naturally, those languages which tried to compensate for their lack of direct word order with declensions were among the most confused of all.
We might bear in mind that, even though, in 1784, while he was writing his pamphlet, de Rivarol was an habitué of Enlightenment circles, after the advent of the revolution, he revealed himself to be a conservative legitimist.
To a man so spiritually tied to the ancien régime, the philosophy and linguistics of the sensationalists may (quite justifiably) have appeared as a harbinger of an intellectual revolution which emphasized the passions as the fundamental force motivating humanity.
If this were the case, then “the direct word order acquires the value of an instrument of protection [ . . . ] against the inflammatory style of the public orators who, in a few short years, would be preaching revolution and manipulating the masses.” (Pellerey 1992a: 147).
Yet what really characterized the eighteenth century debate was the desire not so much to simplify grammar as to show that there existed a natural and normal grammar, universally present in all human languages. This grammar is not, however, manifestly apparent; it must be sought instead beneath the surface of human languages, all of which are, in some degree or other, derivations from it.
As can be seen, we have returned to the ideal of a universal grammar, only now one is trying to identify it by reducing every existing language to its most laconic form.
Attentive as we have been throughout this story to the issue of side-effects, we ought here to note that without this eighteenth century intuition of an original, laconic grammar, our contemporary notions of generative and transformational grammar would be quite inconceivable, even if their origins are usually traced back to the Cartesianism of Port Royal.”
Umberto Eco, The Search for the Perfect Language, translated by James Fentress, Blackwell. Oxford, 1995, pp. 296-302.